夕食の支度で忙しい時間帯、「ママ、この計算教えて!」と子供に言われて、ドキッとしたことはありませんか?
特に分数の計算は、大人でも手順を忘れてしまいがちです。「あれ、どっちをどっちで割るんだっけ?」と焦ってスマホで検索してしまう気持ち、痛いほどよくわかります。
でも、大丈夫です。仮分数を帯分数に直す計算は、難しい数式ではなく「おんぶ」のイメージを持つだけで、子供は驚くほどスムーズに理解できるようになります。
この記事では、スマホを見せるだけで子供が納得する「おんぶメタファー図解」と、親がそのまま読むだけで教えられる「魔法のカンペ台本」をご紹介します。これを読めば、もう「どっちだっけ?」と迷うことなく、自信を持って子供に教えられるようになりますよ。
この記事を書いた人
坂本 あゆみ
元小学校教諭・おうち学習アドバイザー
15年間の教員生活で延べ500人以上の「算数苦手」な児童を指導。現在は二児の母として、ブログやセミナーで「親が教えるコツ」を発信中。「先生」としてではなく、同じ子育て中のママとして、忙しい毎日の中で実践できる学習サポートを提案しています。
なぜ子供は「仮分数→帯分数」でつまずくの?
数字の操作だけを教えると、子供は混乱します
「計算ドリルを何回もやらせているのに、また間違えてる…」
そんなため息をつきたくなること、ありますよね。実は、子供が仮分数を帯分数に直す計算でつまずく最大の原因は、「分母(お母さん)」まで変えてしまうことにあります。
例えば、「$\frac{7}{3}$」を帯分数に直すとき、一生懸命計算するあまり、分母の「3」を別の数字に変えてしまったり、商と余りを書く場所が逆になったりするのです。これは、子供たちが「分数の意味」をイメージできないまま、単なる数字の操作として手順を暗記しようとしているからです。
【体験談】ドリルを繰り返させて失敗した、私の教員時代
恥ずかしながら、私も教員になりたての頃は「習うより慣れろ」だと思っていました。計算手順が定着しない子供たちに、ひたすら計算ドリルを解かせていたのです。
しかし、ある男の子が泣きながらこう言いました。「先生、数字がいっぱいで、何がなんだかわからないよ」。
その時、私はハッとしました。子供たちに必要なのは、大量の演習ではなく、「今、数字たちがどういう状態なのか」を直感的に理解できるイメージだったのです。
💡 専門家の経験からの一言アドバイス
【結論】: 計算手順を教える前に、まずは「分母は絶対に変えてはいけない」というルールを、視覚的なイメージで伝えてあげてください。
なぜなら、この点は多くの人が見落としがちで、子供は計算に集中すると「分母」という土台の存在を忘れてしまうからです。最初に「分母=お母さん」というイメージを共有することで、ケアレスミスは劇的に減ります。この知見が、あなたの成功の助けになれば幸いです。
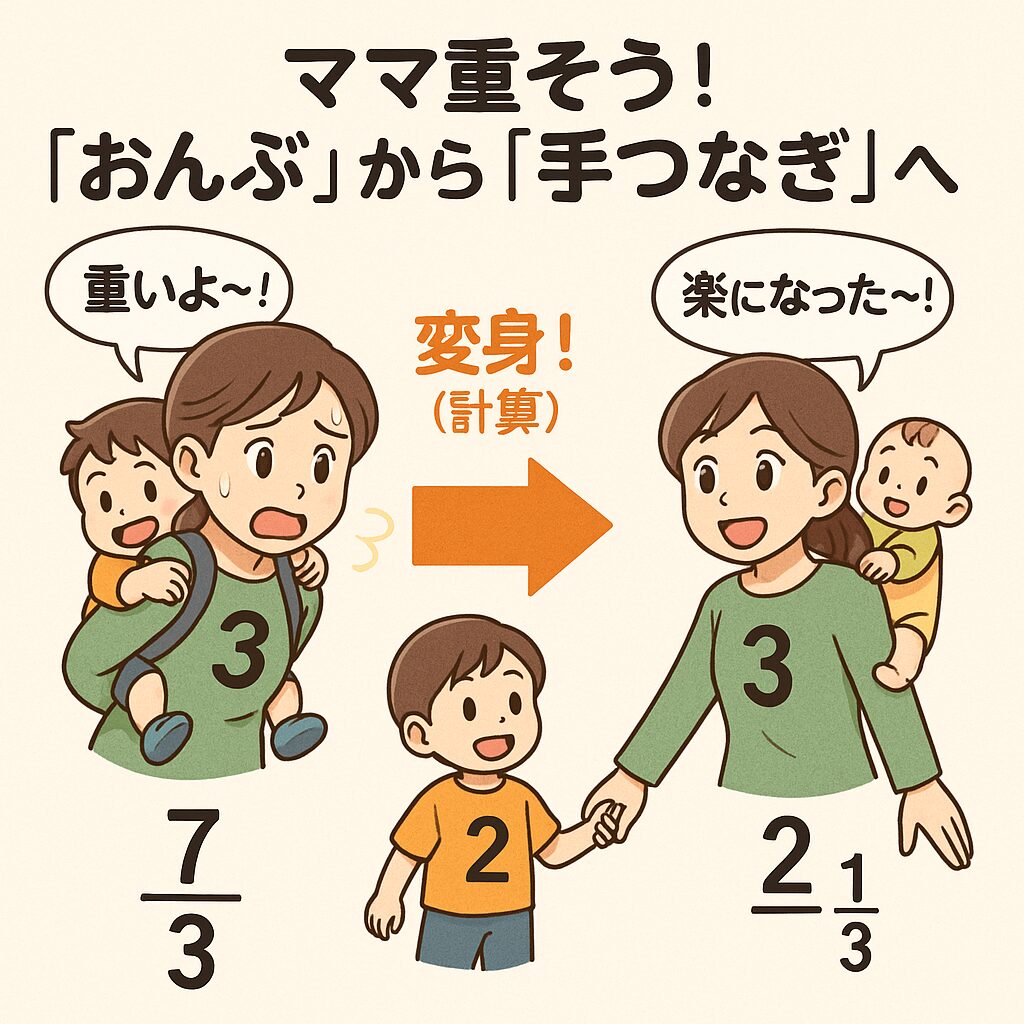
ママ重そう!「おんぶ」で覚える仮分数と帯分数【図解あり】
仮分数は「おんぶ」、帯分数は「手つなぎ」
では、どうすれば子供に伝わるのでしょうか? ここで登場するのが、「おんぶメタファー」です。
この方法では、分数の要素を以下のように見立てます。
- 分母 = お母さん(下で支える土台。絶対に変えてはいけない存在)
- 分子 = 子供(お母さんに乗っている存在)
この関係性を使うと、仮分数と帯分数の違いは次のように説明できます。
- 仮分数($\frac{7}{3}$など):小さなお母さん(3)が、大きな子供(7)をおんぶしている状態です。「うわ?、重そう!グラグラして不安定!」というイメージです。
- 帯分数($2\frac{1}{3}$など):お母さんが子供を降ろして、横に立っている状態です。「あ?、楽ちん!安定したね」というイメージです。
つまり、仮分数を帯分数に直すという計算は、「重そうな仮分数」を「安定した帯分数」に変身させることなのです。形は変わっても、そこにいる「お母さん」と「子供」の人数(量)は変わりません。これが変換・等価の関係です。
魔法の呪文は「上÷下」!間違えない計算手順
リズムで覚える「上÷下=横…余りが上」
イメージができたら、いよいよ具体的な計算手順に入ります。ここでも「お母さん(分母)」の存在が鍵になります。
例として、仮分数の $\frac{7}{3}$ を帯分数に直してみましょう。
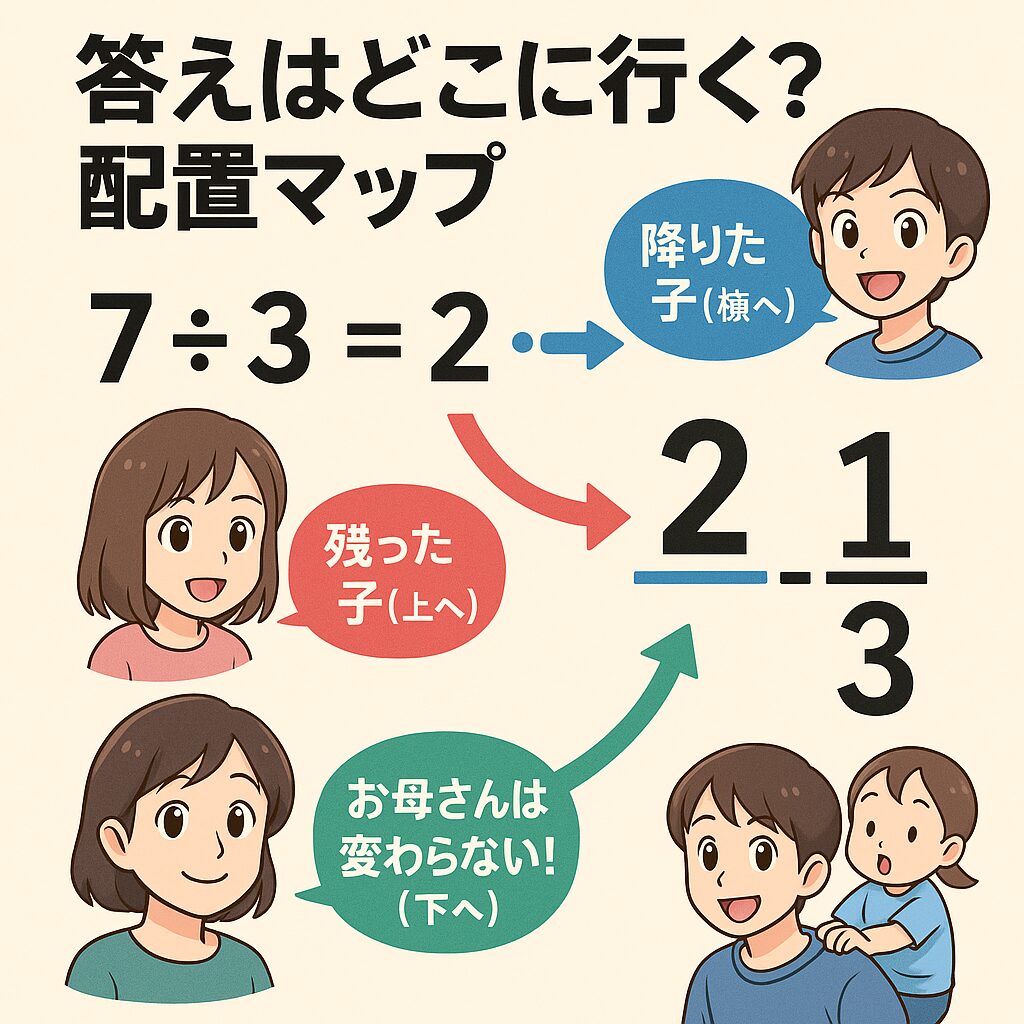
使う魔法の呪文は、「上(子)÷ 下(母)」です。
- 計算式を立てる:
分数の線は「割り算」を表します。上にある分子(7)を、下にある分母(3)で割ります。
$$7 \div 3 = 2 \quad \text{あまり} \quad 1$$ - 答え(商)を横に書く:
割り算の答えである「2」は、おんぶから降りて一人立ちした数です。これを分数の横(整数部分)に大きく書きます。 - 余りを上に書く:
割り切れずに余った「1」は、まだお母さんの背中に残っている数です。これを新しい分子(上)に書きます。 - 分母はそのまま!:
ここが最重要ポイントです。分母(お母さん)の「3」は、絶対に変えずにそのまま下に書きます。お母さんは計算しても変わりません。
これで、$2\frac{1}{3}$ の完成です。
そのまま読める!親のための「教え方カンペ」
夕食前の忙しい時間、頭の中で整理してから教える余裕なんてないですよね。
そんな時は、この「教え方カンペ」をスマホで見ながら、そのままお子さんに読んであげてください。
【親御さん用スクリプト】
ママ: 「ねえねえ、この分数($\frac{7}{3}$)、頭が大きくてちょっと重そうだよね?」
子供: 「うん、上が大きいね」
ママ: 「これ、小さなお母さんが、大きな子供をおんぶしてるみたいじゃない? 重くて大変そうだから、おんぶから降ろしてあげようか」
子供: 「どうやって?」
ママ: 「『上÷下』で計算するんだよ。7の中に3は何人いるかな? 割り算してみて」
子供: (計算して)「2あまり1!」
ママ: 「正解! その『2』は、おんぶから降りて横に立てる人数だよ。だから横に大きく『2』って書いて」
子供: (書く)
ママ: 「で、余った『1』は、まだおんぶのままだから、上に『1』って書こう」
ママ: 「最後に、下のお母さん(3)はどうするんだっけ?」
子供: 「お母さんは変わらない!」
ママ: 「その通り! だから下はそのまま『3』だね。これでスッキリした形になったね!」
よくある質問 (FAQ)
Q. 割り切れたらどうするの?
A. おんぶ終了! 整数だけになります。
例えば $\frac{6}{3}$ の場合、$6 \div 3 = 2$ で余りがありません。これは「全員おんぶから降りられた」状態です。分数はなくなり、答えは整数の「2」だけになります。
Q. 必ず帯分数に直さないといけないの?
A. 問題の指示によりますが、量の大きさを知るには帯分数が便利です。
「$\frac{7}{3}$リットル」と言われるより、「$2\frac{1}{3}$リットル(2リットルとちょっと)」と言われた方が、どれくらいの量かイメージしやすいですよね。計算の答えとしては仮分数のままでも正解の場合が多いですが、帯分数は「量の感覚」をつかむのに役立つと教えてあげてください。
まとめ
仮分数を帯分数に直す計算は、単なる数字のパズルではありません。
「重そうな仮分数」を「安定した帯分数」にしてあげるという目的と、「お母さん(分母)は変わらない」というルールさえイメージできれば、子供たちはもう迷いません。
- イメージ: おんぶ(仮分数)から、手つなぎ(帯分数)へ
- 呪文: 上 ÷ 下
- 鉄則: お母さん(分母)は絶対に変えない!
お母さんが「なるほど!」と納得して説明できれば、その安心感はお子さんにも必ず伝わります。ぜひ、この記事の図解をそのままお子さんに見せて、「重そうだね、降ろしてあげようか?」と声をかけてみてください。きっと、「わかった!」という笑顔が見られるはずです。
参考文献
- 仮分数・帯分数の直し方-そもそもどっちだっけ?にも答えます - できる子ども育成塾
- わかりやすい分数の教え方のポイント - がんプリ